Complex Disordered Systems

Active Matter

Francesco Turci

Today

Beyond thermal equilibrium
Run-and-tumble dynamics
Active Brownian particles
Motility-induced phase separation (MIPS)

Beyond Thermal Systems

Equilibrium systems systems:

Free energy is optimised (subject to constraints):
Distribution of states given by Boltzmann statistics: P(\text{state}) \propto e^{-E(\text{state})/k_BT}

Arrested systems

Supercooled liquids: local equilibrium (thermal)
Glasses/gels: slow relaxation (towards equilibrium)

Active matter: Nonequilibrium via local dissipation

Local energy consumption
Self-propulsion
Dissipation at microscopic scale

Examples:

Bacteria
Synthetic microswimmers
Molecular motors
Bird flocks, fish schools

In a active systems, the distribution of states is not given by Boltzmann statistics!

Examples of Active Matter

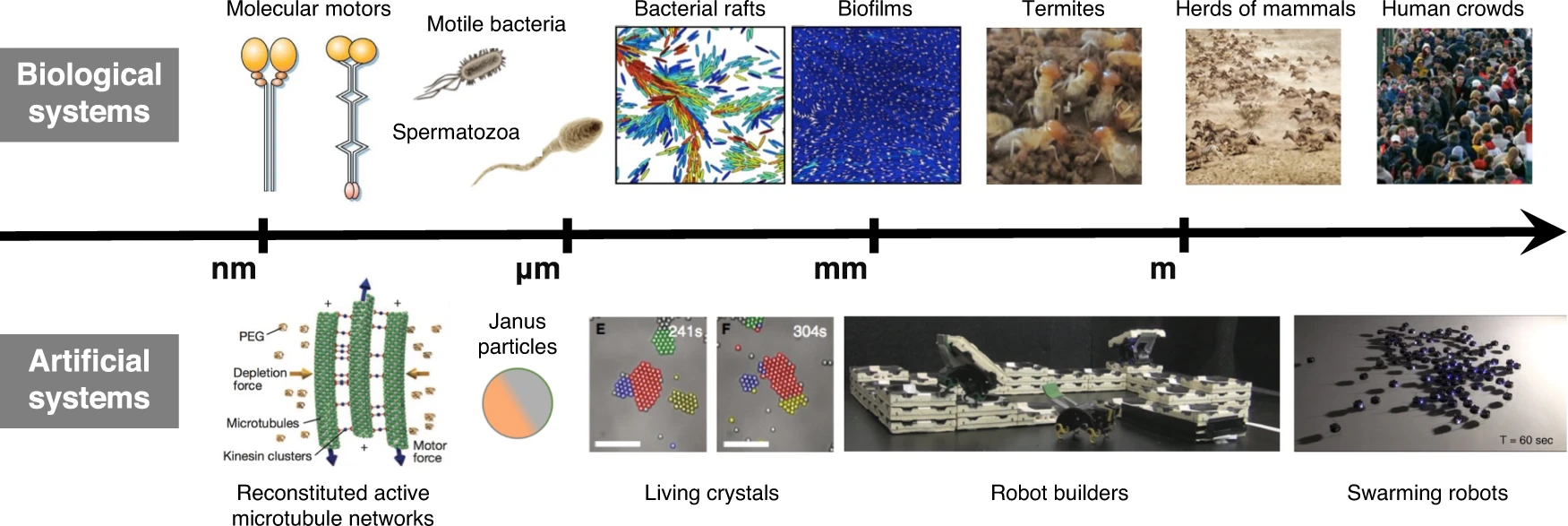
Some examples Active matter examples, from Vole et al. npj Microgravity (2022)

Flocking as a minimal model

The Vicsek model (1995) was one of the simplest models of active matter. Key ingredients: alignment + self propulsion

N particles with positions \mathbf{r}_i and orientations \theta_i
Update rules: \mathbf{r}_i(t+1) = \mathbf{r}_i(t) + v_0 \hat{\mathbf{n}}_i(t) \theta_i(t+1) = \langle \theta_j \rangle_{|\mathbf{r}_j - \mathbf{r}_i| < R} + \eta_i
v_0: constant speed
R: interaction radius
\eta_i: noise term (uniform random in [-\pi/2, \pi/2])

Flocking as a minimal model

Vicsek simulation

Run-and-Tumble Motion

Further inspirations from the microbial world, where dissipation can be more directly observed (and even tuned).

Inspired by bacterial motion (E. coli)

Two phases:

Run: Straight-line motion at constant speed v_0
Tumble: Random reorientation

Key parameter: Tumble rate \lambda

Run-and-Tumble: Dynamics

Code

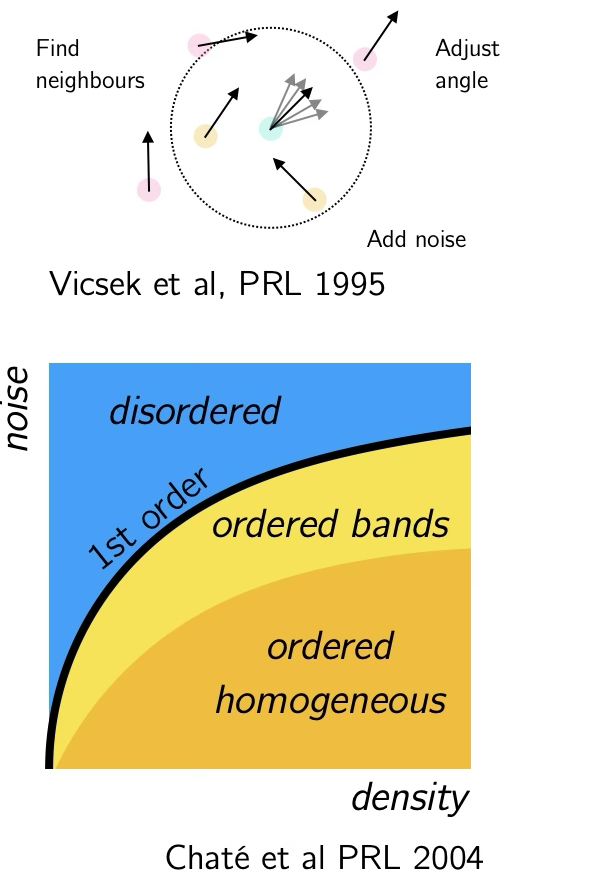
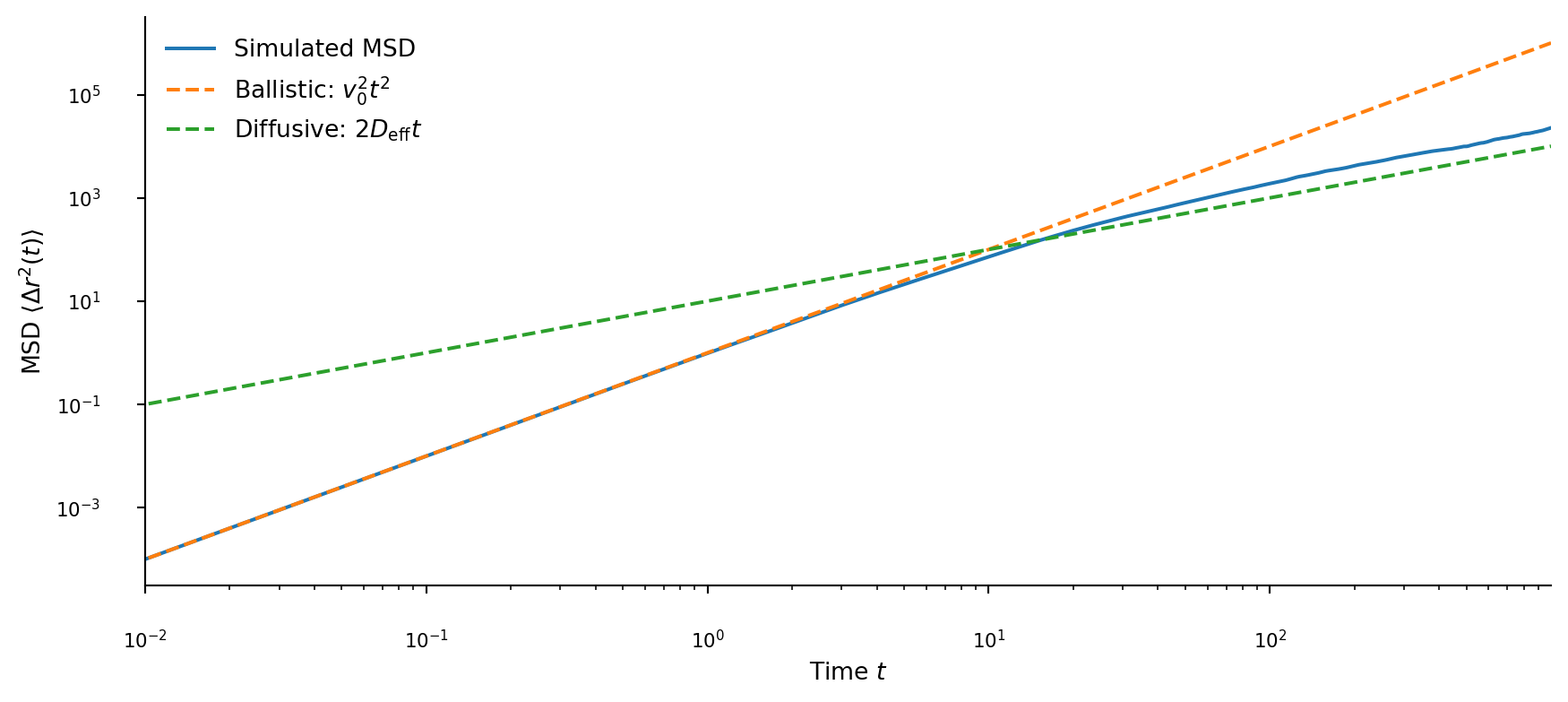
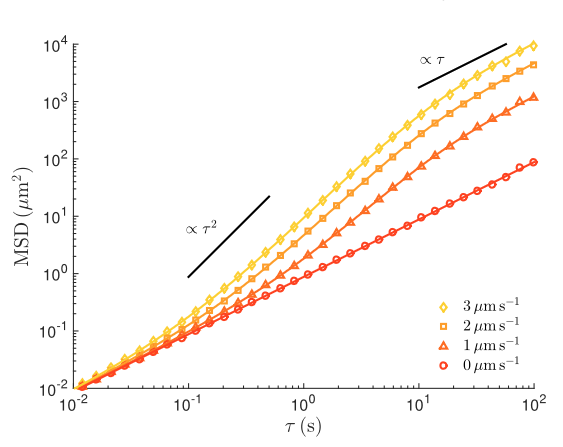
viewof simulation = {
    const n = 300, W = 1000, H = 500, dt = 0.5, v0 = 1.5;

    const tumbleSlider = Inputs.range([0.01, 1.0
    ], {step:0.01, value:0.1, label:"Tumble rate λ"});
    const button = html`<button>Pause</button>`;
    let running = true;
    button.onclick = () => {
        running = !running;
        button.textContent = running ? "Pause" : "Resume";
    };

    let state = Array.from({length: n}, () => ({
        x: Math.random() * W,
        y: Math.random() * H,
        theta: Math.random() * 2 * Math.PI
    }));

    // Each particle gets a trace array
    let traces = Array.from({length: n}, () => []);

    // Reset traces when tumble rate changes
    let lastLambda = tumbleSlider.value;
    tumbleSlider.addEventListener("input", () => {
        traces = Array.from({length: n}, () => []);
        lastLambda = tumbleSlider.value;
    });

    function step(state, λ) {
        return state.map((p, i) => {
            if (Math.random() < λ * dt) p.theta = Math.random() * 2 * Math.PI;

            // Predict next position
            let nx = p.x + v0 * Math.cos(p.theta) * dt;
            let ny = p.y + v0 * Math.sin(p.theta) * dt;

            // Bounce at left/right walls
            if (nx < 0) {
                p.x = 0;
                p.theta = Math.PI - Math.random() * Math.PI; // random angle pointing right
            } else if (nx > W) {
                p.x = W;
                p.theta = Math.PI + Math.random() * Math.PI; // random angle pointing left
            } else {
                p.x = nx;
            }

            // Bounce at top/bottom walls
            if (ny < 0) {
                p.y = 0;
                p.theta = (Math.random() * Math.PI); // random angle pointing down
            } else if (ny > H) {
                p.y = H;
                p.theta = Math.PI + (Math.random() * Math.PI); // random angle pointing up
            } else {
                p.y = ny;
            }

            // Add current position to trace
            traces[i].push([p.x, p.y]);
            // Limit trace length for performance
            if (traces[i].length > 200) traces[i].shift();
            return p;
        });
    }

    const container = html`<div></div>`;
    container.append(tumbleSlider, button);
    const svg = d3.select(container).append("svg")
        .attr("width", W)
        .attr("height", H)
        .style("background", "#f8f8f8");

    while (true) {
        const λ = tumbleSlider.value;
        if (running) state = step(state, λ);

        svg.selectAll("*").remove();

        // Draw traces
        traces.forEach(trace => {
            if (trace.length > 1) {
                svg.append("path")
                    .attr("d", d3.line()(trace))
                    .attr("stroke", "#90caf9")
                    .attr("stroke-width", 1)
                    .attr("fill", "none");
            }
        });

        // Draw particles
        svg.selectAll("circle")
            .data(state)
            .enter().append("circle")
            .attr("cx", d => d.x)
            .attr("cy", d => d.y)
            .attr("r", 3)
            .attr("fill", "#1976d2");

        svg.selectAll("line")
            .data(state)
            .enter().append("line")
            .attr("x1", d => d.x)
            .attr("y1", d => d.y)
            .attr("x2", d => d.x + 10 * Math.cos(d.theta))
            .attr("y2", d => d.y + 10 * Math.sin(d.theta))
            .attr("stroke", "#1976d2")
            .attr("stroke-width", 1.2);

        yield container;
        await Promises.delay(16);
    }
}

Figure 1: Non-interacting run and tumble particles.

Run-and-Tumble dynamics

Run phase (constant velocity): \mathbf{r}(t + \Delta t) = \mathbf{r}(t) + v_0 \hat{\mathbf{n}}(t) \Delta t

Tumble phase (random reorientation):

With probability \lambda \Delta t: randomize \hat{\mathbf{n}}
Otherwise: continue running

Mean Squared Displacement

Two regimes

Ballistic (short times): \langle \Delta r^2(t) \rangle \sim v_0^2 t^2
Diffusive (long times, t \gg 1/\lambda): \langle \Delta r^2(t) \rangle \sim 2 D_{\text{eff}} t
- Effective diffusion: D_{\text{eff}} = \frac{v_0^2}{2\lambda} (2D)

Crossover time: t_c \sim 1/\lambda

Active Brownian Particles (ABPs)

Minimal model for self-propelled colloids (e.g., Janus particles)

Dynamics:

Translational motion \frac{d\mathbf{r}}{dt} = v_0 \hat{\mathbf{n}}(t) + \sqrt{2D_t} \boldsymbol{\xi}(t)
Rotational motion \frac{d\theta}{dt} = \sqrt{2D_r} \eta(t)

v_0: self-propulsion speed
D_t: translational diffusion
D_r: rotational diffusion
Continuous reorientation

Péclet Number: Pe = \frac{v_0}{\sqrt{D_t D_r}} = \frac{v_0}{D_r L}

Measures activity strength vs thermal motion
Pe \ll 1: thermal equilibrium limit
Pe \gg 1: strong activity, far from equilibrium
L = \sqrt{D_t/D_r}: characteristic length scale

ABP: Mean Squared Displacement

Three regimes:

\langle \Delta r^2(\tau) \rangle = \left[4 D_T + 2 v^2 \tau_R \right] \tau + 2 v^2 \tau_R^2 \left( e^{-\tau / \tau_R} - 1 \right)

Short times: Diffusive \sim 4D_T\tau
Intermediate: Ballistic \sim v_0^2\tau^2
Long times: Enhanced diffusion

\tau_R = 1/D_r: persistence time
D_{\mathrm{eff}} = \frac{v_0^2}{2D_r}: effective diffusion

Mean squared displacement for ABPs at different self-propulsion speeds.

Effective Interactions

The persistence of active motion can lead to effective interactions between particles.

Head-to-head collisions lead to a persistence time of contact between two particles
This can be seen as an effective attraction between particles

Effective twobody potential for ABPs, Turci & wilding PRl 2021

(The realiity is more complex, with many-body effects!)

Motility-Induced Phase Separation (MIPS)

Interacting ABPs → nonequilibrium self-organization

MIPS in 3D ABPs from Turci and Wilding Physical Review Letters 2021

Key idea: Purely repulsive particles (hard spheres) + ABP dynamics

MIPS Mechanism

Equilibrium (no self-propulsion):

Hard spheres
No liquid-gas separation

Active (with self-propulsion):

Head-to-head collisions
Finite residence time
Many-body caging
Density heterogeneities

As D_r decreases:

More persistent motion
System more out-of-equilibrium
Enhanced density fluctuations
Spontaneous phase separation

MIPS: Critical-like Behavior

Phase diagram features:

Low D_r: Dense + dilute phases (like liquid-gas)
Critical point: Enhanced fluctuations
MIPS exists both in 2d and 3D:
- in 2D, disk ordering at high densities
- in 3D, MIPS is metastable to gas-crystal, like colloid polymer mixtures.
Short-range effective interactions between active particles

Result: Nonequilibrium phase transition in purely repulsive system!

Experimental realisation of active matter

In experiments, active systems can be realised in various ways:

Bacterial suspensions: e.g., E. coli, B. subtilis
Synthetic microswimmers: Janus particles with catalytic coatings
Light-activated colloids: Particles that change motility under light

Vibrated granular matter: Macroscopic particles on vibrating plates
Nano- and micro-robots: Swarms of tiny robots with programmed motion

Experimental systems and active. matter behaviours