Complex Disordered Systems

Gelation

Francesco Turci

Today

• Physical gels and percolation
• Colloid-polymer mixtures
• Structure and characterization
• Arrested spinodal decomposition

What is a Physical Gel?

Physical gel: Particles/polymers connected via reversible, non-covalent bonds forming a percolating network

Key features:

• Bonds break/reform dynamically
• Energy ~ k_BT
• Self-healing possible
• Thermoreversible

Examples:

• Gelatin
• Agarose
• Yoghurt
• Paint, inks

Cross-links form via dense local regions (microcrystalline/glassy)

Physical vs Chemical Gels

Physical Gels

• Reversible bonds
• Energy ~ k_BT
• Dynamic network
• Thermoreversible

Chemical Gels

• Irreversible covalent bonds
• High energy barriers
• Permanent network

Key transition:

• Fluid → Gel occurs when a system-spanning cluster forms (percolation)
• Dramatic viscosity increase + elastic response

Gels are a second example of disordered solids (after glasses)

Percolation Theory

Problem: Square grid L\times L sites, randomly label N of them. When does a spanning cluster form?

• p = N/L^2 = occupation probability
• Percolation threshold p_c
• Below p_c: small clusters
• Above p_c: giant spanning cluster

2D square lattice: p_c \approx 0.5927

Transition: Continuous (2nd order)

Percolation Simulation

Percolation Transition

Percolation Threshold: p_c Values

Non-universal: p_c depends on lattice type and dimension

Lattice	Dim	z	p_c^{site}	p_c^{bond}
Square	2	4	0.593	0.5
Triangular	2	6	0.5	0.347
Cubic	3	6	0.312	0.249
Hypercubic	4	8	0.197	0.160
Hypercubic	6	12	0.109	0.094

Higher dimensions → lower p_c (easier to percolate)

Critical Exponents: Universal

Universal: Critical exponents independent of lattice details

P_{\infty}(p)\propto (p-p_c)^{\beta}

Dimension d	\beta
2	5/36 ≈ 0.14
3	≈ 0.41
≥6	1 (mean-field)

Gels require percolation for mechanical stability!

Colloidal Gel Formation

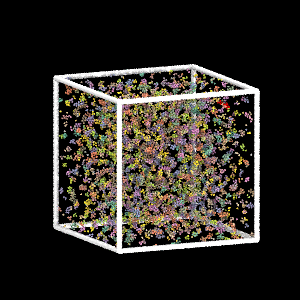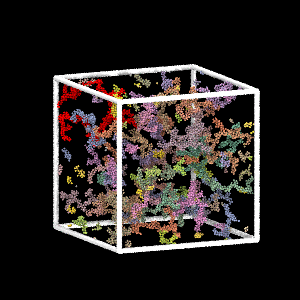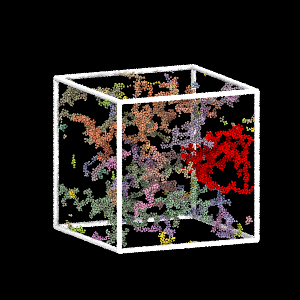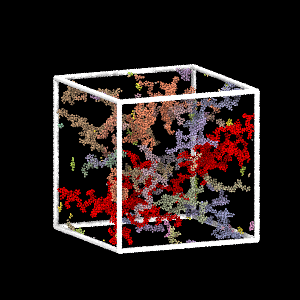
MD simulation of dilute colloidal gel formation (largest cluster in red)

Percolating cluster → mechanical rigidity

Colloid-Polymer Mixtures

Depletion interactions like the Asakura-Oosawa model produce a very short ranged potential with strong attractive part. W_{\mathrm{AO}}(r)=-\frac{4 \pi \rho_p k_B T}{3} R^3(1+q)^3\left[1-\frac{3}{4} \frac{r}{R(1+q)}+\frac{1}{16}\left(\frac{r}{R(1+q)}\right)^3\right], \quad 2R<r<2(R+R_p), \quad q=\dfrac{R_p}{R}

attractive + very short ranged → sticky interaction

• Colloids cluster into nonequilibrium branched phase
• Binodal becomes metastable to fluid-solid coexistence

Phase diagram of colloid-polymer mixtures for varying polymer-colloid aspect ration q. Small

Simple Model Potentials

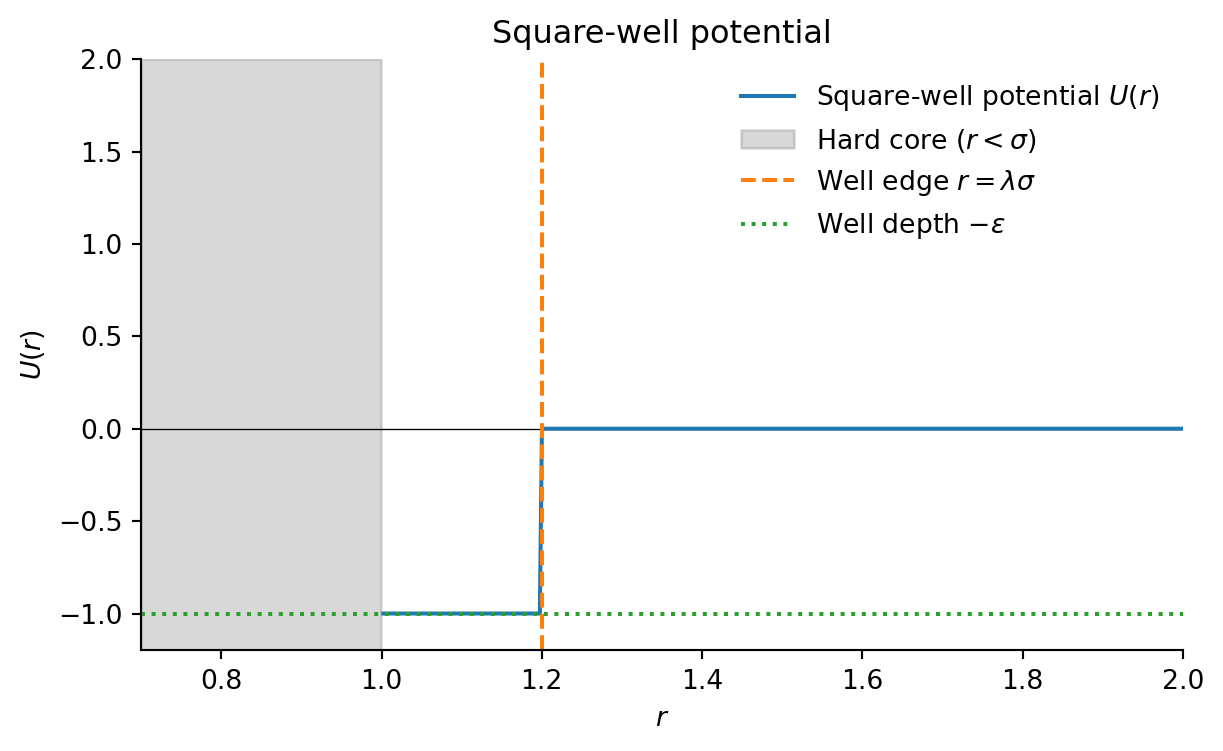
Square-well potential:

U(r) = \begin{cases} \infty & r < \sigma \\ -\epsilon & \sigma \leq r < \lambda \sigma \\ 0 & r \geq \lambda \sigma \end{cases}

• \sigma: particle diameter
• \epsilon: well depth
• \lambda: range parameter

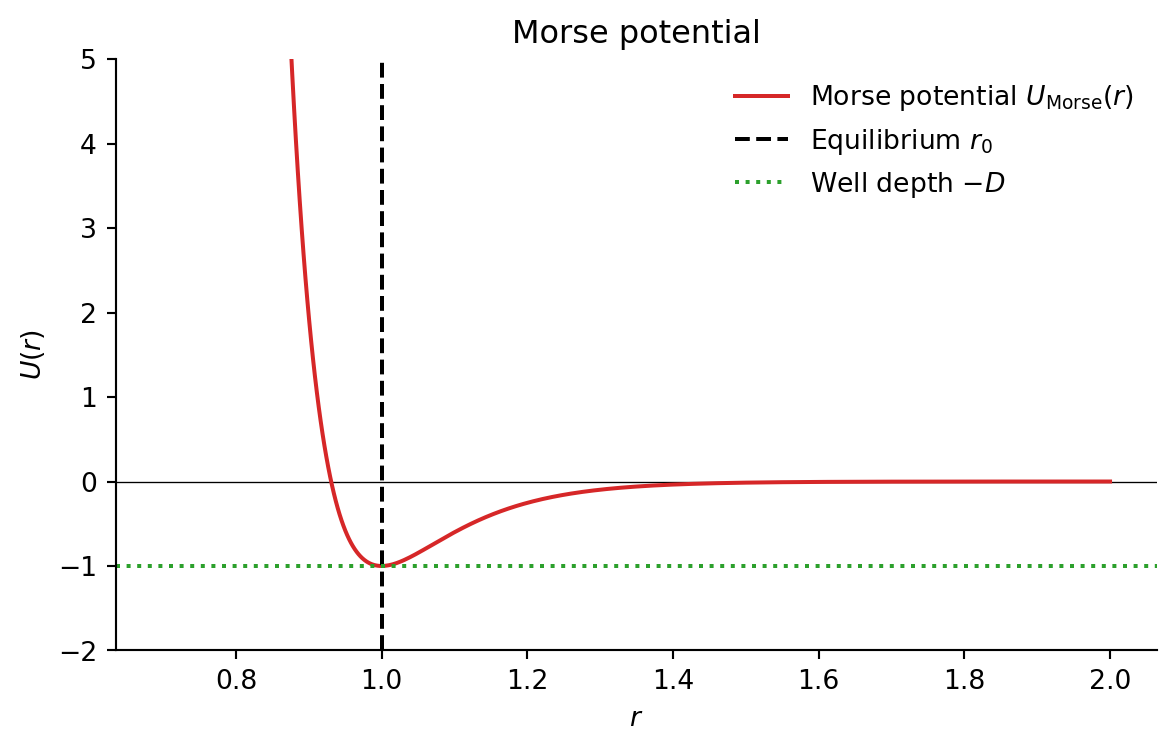
Morse Potential (MD Simulations)

Smooth short-range attractive potential:

U_{\mathrm{Morse}}(r) = D \left[ e^{-2\alpha (r - r_0)} - 2 e^{-\alpha (r - r_0)} \right]

• D: well depth
• \alpha: steepness (controls range)
• r_0: equilibrium distance

Pair Correlations: g(r)

Radial distribution function g(r): best at short distances

• Captures cluster structure
• Sharp peaks at dilute concentrations
• Nearest/second-nearest neighbor shells

Time evolution of g(r) ina dilute gel in units of the time to percolate \tau_{\mathrm perc}

Structure Factor: S(q) and Fractals

Near percolation threshold, the loq-q trend from the trsucture factor links to the compressibility: power-law behavior:

Clusters become fractal objects with self-similar structure at all length scales.

For a fractal object with dimension D_f:

• Mass scales as M(R) \sim R^{D_f}
• Density correlations decay as \rho(r) \sim r^{-(d-D_f)}

Fourier transform of power-law correlations gives: S(q) \sim q^{-D_f}

• D_f: fractal dimension
• No characteristic length scale
• Typical 3D: D_f \approx 2.5

Time evolution of the structure factor S(q)

Arrested Spinodal Decomposition

How do gels form?

Scenario:

1. Rapid quench into unstable region
2. Phase separation begins (spinodal)
3. Dense regions arrest (glass/jamming)
4. Bicontinuous frozen structure

The picture suggest the progressive freezing of coarsening upon spinodal decomposition.

Phase Diagram: Arrested Spinodal

Arrested spinodal scenario, see Zaccarelli et al 2007

Key lines:: - Binodal (red): liqiid-gase coexistence at equilibrium - Spinodal (dashed): limit of stability of the metastable phases. Instability (i.e. spinodal decomposition) starts inside - Percolation (purple): At some density, the clusters percolate (span the system) - Glass transition (blue): Dense phase becomes dynamically arrested (non-ergodic)

Gel path: Rapid cooling → arrested dense phase + vapor