More on wetting in very large systems with cross-shaped geometry
VERY large systems with cross-shaped geometry
I pushed the simulations a bit further and simulated very large 3D systems with $L_x = L_y = 120\sigma$ and a thinner transverse dimension $L_z = 20\sigma$, at density $\rho=0.75$ so that I simulate N = 216000 particles for 300$\tau_r$.

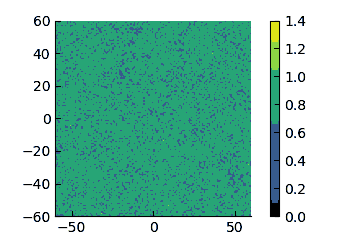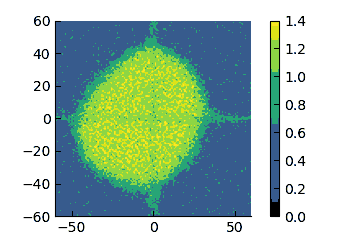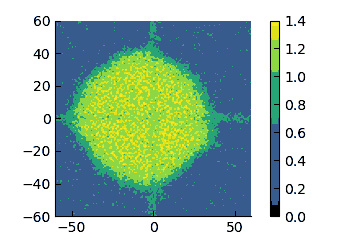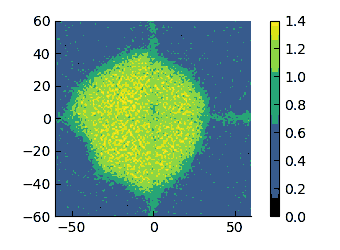
Density field at $\varepsilon=8$ in a system with size $L_x=120\sigma$.
The following animations illustrate the relaxation to the steady state at different barrier strengths
| $\varepsilon=8$ | $\varepsilon=10$ | $\varepsilon=20$ | $\varepsilon=30$ |
|---|---|---|---|
 |
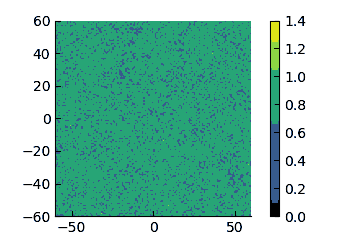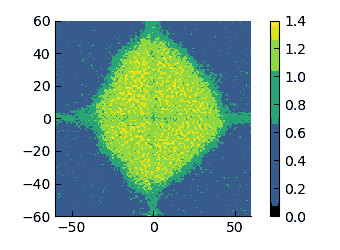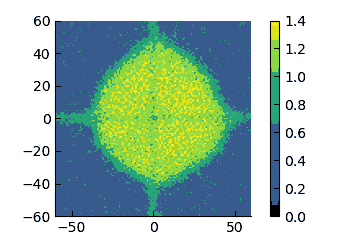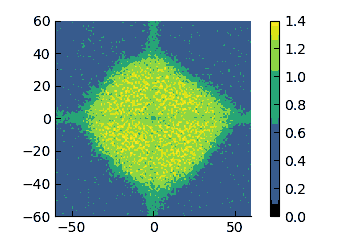 |
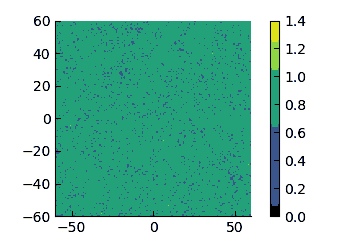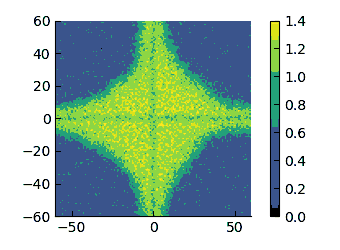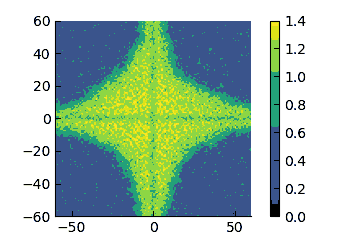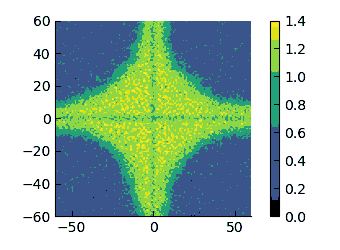 |
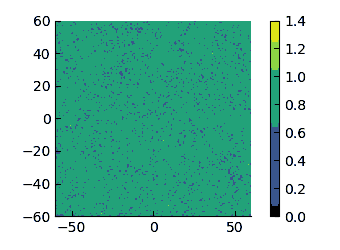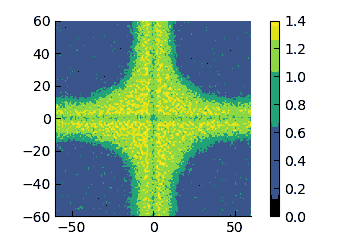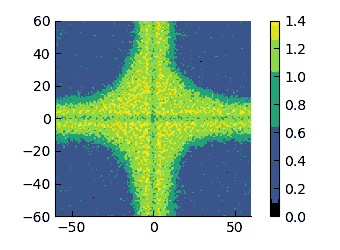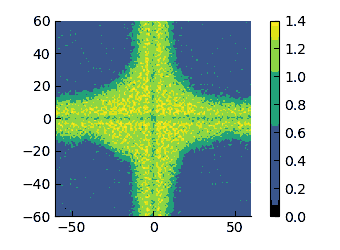 |
There is some asymmetry in the profiles at low $\varepsilon$ but - as we have previously discussed - it is made probably rather complex by cross interactions across quadrants.
On these scales, I think that it appears more evident that the low-density region changes from having a convex interface (high $\varepsilon$) to a concave one (low $\varepsilon$). therefore, I have tried to quantify the curvature of these interfaces.
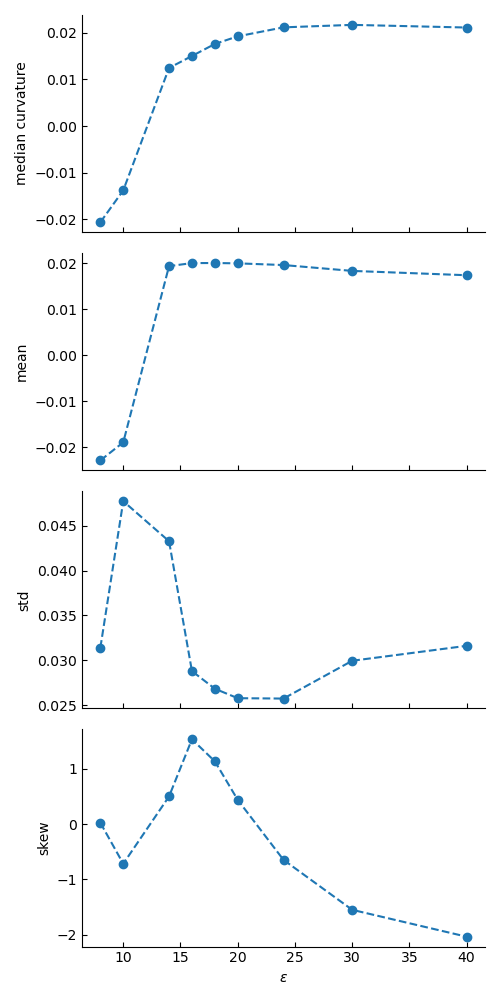
Curvatures
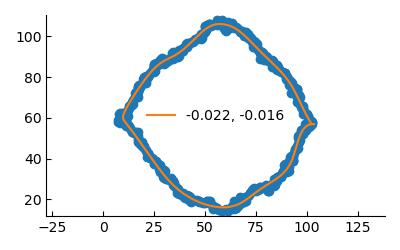
I use a level set to identify the curvature. I coarse grain the density (as in the videos above) and choose a level set at the diameter density $\rho_{diam}=0.85$. This defines segmented curves in 2D through which I can fit a spline curve to extract the curvature at every point. I can then associate a curvature value to every contour either by taking the average of the curvatures or the median. Since, in fact, the curves present some pointed regions at small epsilons, some outliers need to be removed to compute the mean.
| $\varepsilon=10$ | $\varepsilon=40$ |
|---|---|
 |
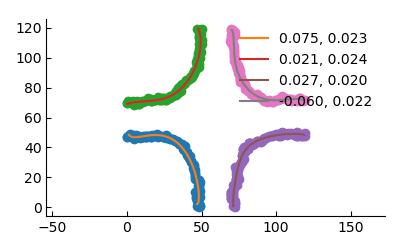 |
The probability distribution function of the curvature at steady state is non-Gaussian.
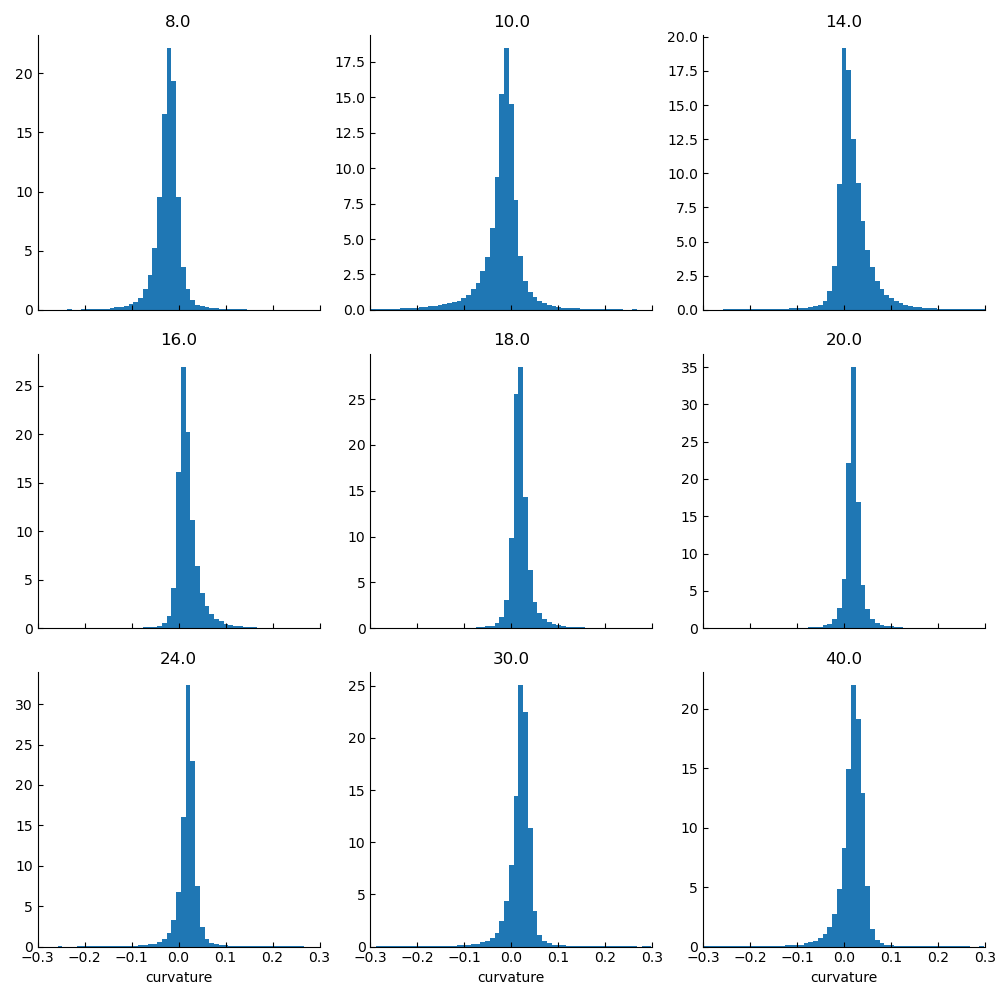
The curvature captures aspects of the transition (again, the order is not clear). Noticeably, there is essentially an inversion in the sign of the curvature (both median and mean). Note that the mean displays a non-monotonic behaviour, which seems consistent with the fact that at large $\varepsilon$ the interface is mostly flat away from the centre (so the curvature should be closer to zero).