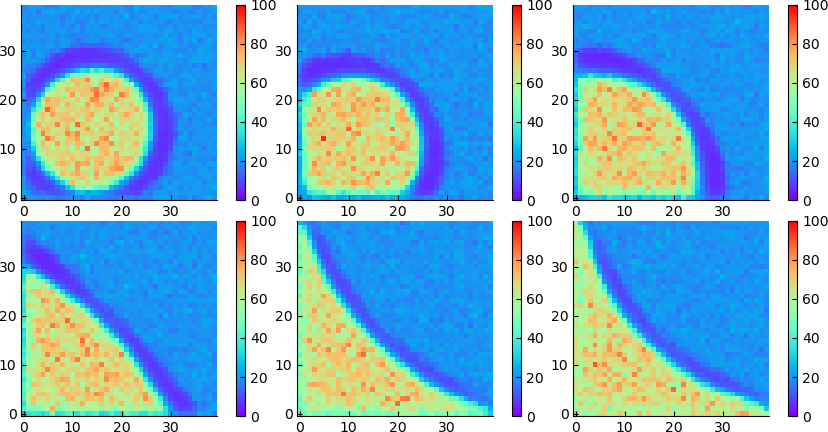
Wetting in corner geometry: passive LJ
Passive wetting of LJ particles in a corner
To understand better what can be calculated in the active case, I went back to the passive case of Lennard-Jones particles but constrained in a similar corner geometry.
The geometry is the following:
- two walls with 9-3 Lennard-Jones interaction at x=0 and y=0 with identical potential well (attraction strength $\epsilon$)
- periodic boundary conditions in the z dimension and reflective boundary conditions in the remaining faces of the cubic box.
- the fluid-fluid interactions are truncated (not shifted) at $2.5\sigma$
## Density
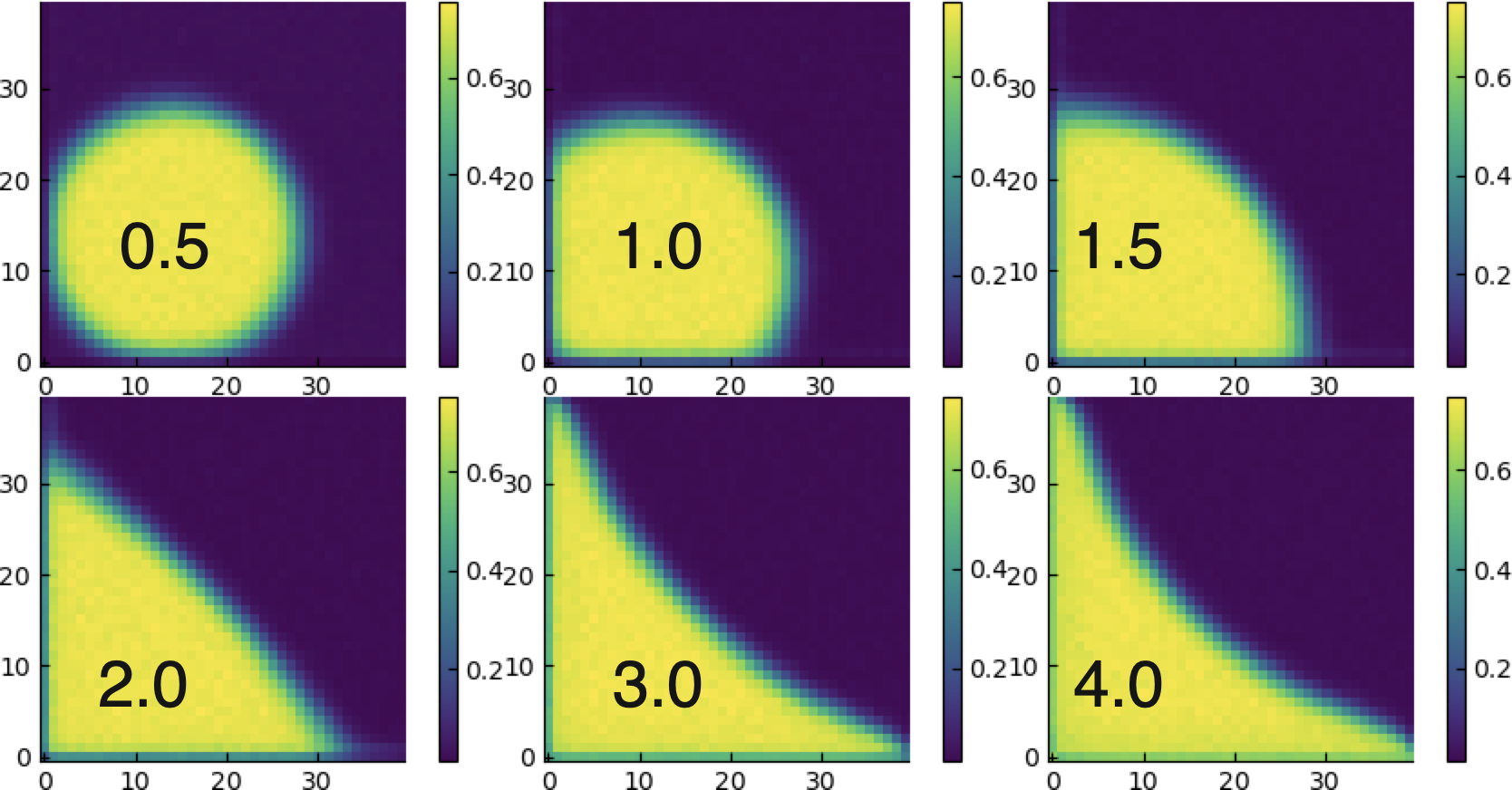
The density profiles are very similar to what we observed in the active case. With decreasing $\epsilon$ (black label)
- The interface goes from convex to concave (eventually, spherical)
- The walls go from fully to partially covered (wet)
- For intermediate values we observe a 90˚ contact angle
- For smaller values the droplet pinches off from the corner: the corner dries
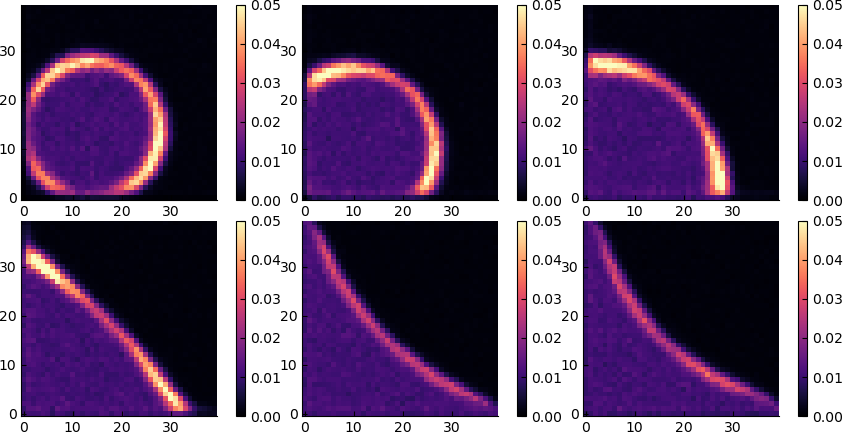
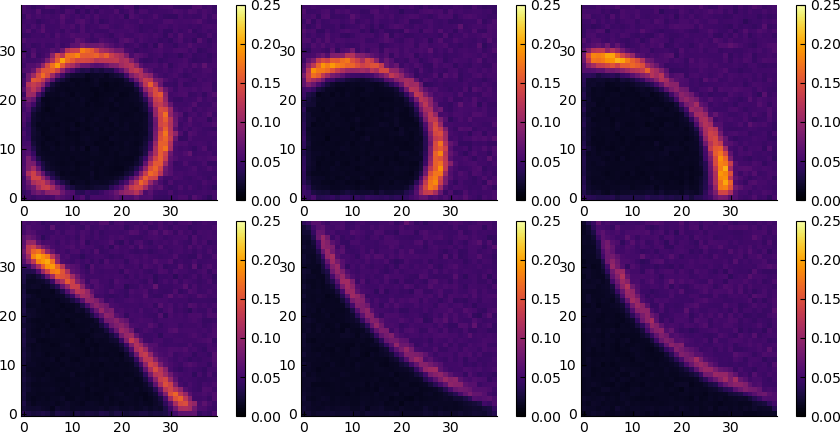
Fluctuations and compressibility
The fluctuations are also qualitatively similar to the active case.
Variance
Compressibility
Possible measures
For this passive system, we can measure the tensions from the anisotropy of the pressure tensor. At contact angle $\theta_c = 90˚$ , $\gamma_{wl}=\gamma_{wg}$ so we should be able to verify this condition. The question is, how does this equality transform for quantities that are accessible also in the active case? For example, does it translate into a relationship for the compressibility field?
Digging the old literature, it seems that there have been well-established empirical observations, including work by Egelstaff and Widom stating that
\[\gamma_{lg}\kappa\sim constant\]where $\kappa$ is the compressibility and $\gamma_{lg}$ is the liquid-vapour surface tension. Other work by Sanchez (JCP 1983) claims, using a square gradient theory for the free energy, that
\[\gamma_{lg}(\kappa/\rho)^{1/2}\sim constant\]with a constant independent of the temperature and $\rho$ being the mass density.
These relations hold for the bulk tension, and are suggestive of a connection between tension and inverse compressibility.
In Young’s equation, the tension is
\[\gamma_{lg}= \dfrac{\gamma_{wg}-\gamma_{wl}}{\cos\theta_c}\]If truly $\gamma_{lg}\sim \kappa^{-1}$ (or a similar negative exponent) it is suggestive that (where the surface of the droplet is far from the walls), the inverse compressibility should measure (scaled) differences in the tensions at the wall.
The maxima of the compressibility are then regions of minimal tension, and the map of the inverse compressibility maybe can guide us in exploring new definitions of suitable observables.