Curve generation and free energy
Notes to find the equal area condition for the Fourier coefficients
I use Rob’s notes on equal area contours.
I start from the condition for equal area
\[\begin{align} \int_{-\phi}^{+\phi}\delta r d\theta = -\dfrac{1}{2R}\int_{-\phi}^{+\phi}\delta r^2 d\theta \label{eq:area} \end{align}\]The RHS is negative. From LHS we understand that the negative contributions $\delta r$ to the path $r(\theta)=R+\delta r(\theta)$ outnumber the positive ones.
I note also that the condition above means that the LHS can not be zero unless $\delta r(\theta)=0$ for all $\theta$.
We assume a form for $\delta r$
\[\delta r (\theta)= \sum_{n=1}^K a_n \sin\left[\dfrac{\pi n (\theta+\phi)}{2\phi}\right]\]which means that at the contact points $\delta r =0$.
We first plug this into the LHS of the starting equation $\ref{eq:area}$
\[\begin{align} \int_{-\phi}^{+\phi}\delta r d\theta &= \int_{-\phi}^{+\phi}\sum_{n=1}^K a_n \sin\left[\dfrac{\pi n (\theta+\phi)}{2\phi}\right]d\theta\\ &= \sum_{n=1}^K \int_{-\phi}^{+\phi}a_n \sin\left[\dfrac{\pi n (\theta+\phi)}{2\phi}\right]d\theta\\ & = \sum_{n=1}^K a_n\left[ -\dfrac{2 \phi}{\pi n} \cos(\frac{\pi n (\phi + x)}{2 \phi}) \right]_{-\phi}^{\phi}\\ & =\sum_{n=1}^K a_n\left[ (\cos(0) - \cos(n\pi) )\dfrac{2 \phi}{\pi n} \right]\\ & = \sum_{i=0}^{K/2} a_{2i} \times0 +\sum_{j=0}^{K/2}\frac{4a_{2j+1} \phi}{\pi (2j+1)} \end{align}\]So, only the odd terms in the series contribute to the integral along the $\delta r$. This makes sense, as the even terms have an equal number of oscillations above and below R, so their contributions cancel out.
I now deal with the RHS of $\ref{eq:area}$. \(\begin{align} RHS = -\dfrac{1}{2R}\int_{-\phi}^{+\phi}\delta r^2 d\theta=-\dfrac{1}{2R}\int_{-\phi}^{+\phi}\left\{\sum_{n=1}^K a_n \sin\left[\dfrac{\pi n (\theta+\phi)}{2\phi}\right]\right\}^2 d\theta\\ \end{align}\)
for convenience, let us define
$u= \dfrac{\pi (\theta+\phi)}{2\phi}$
with $du=\pi d\theta/2\phi$
So \(RHS =-\dfrac{2\phi}{2\pi R}\int_{0}^{\pi}\left\{\sum_{n=1}^K a_n \sin(n u)\right\}^2 du\)
Define
\[I= \int_{0}^{\pi}\left\{\sum_{n=1}^K a_n \sin(n u)\right\}^2 du\]Remember that we have orthogonality \(\int_0^{\pi}\sin(jx) \sin(kx) dx = 0 \quad \rm{for} \quad k\neq j\)
So, only terms with the same index $n$ will deliver nonzero integrals. Therefore \(\begin{align} I &= \int_0^{\pi}\sum_{n=11}^K a_n^2\sin^2(nu) du\\ &= \sum_{n=1}^K a_n^2\int_0^{\pi}\sin^2(nu) du = \dfrac{\pi}{2}\sum_{n=a1}^K a_n^2 \end{align}\)
The initial equation now reads
\[\begin{align} LHS &= RHS\\ \sum_{j=0}^{K/2}\frac{4a_{2j+1} \phi}{\pi (2j+1)} &= -\dfrac{2\phi}{2\pi R}\dfrac{\pi}{2}\sum_{n=1}^K a_n^2 \end{align}\]The $\phi$-dependence drops out \(\sum_{j=0}^{K/2}\frac{4a_{2j+1} }{\pi (2j+1)} = -\dfrac{1}{2 R}\sum_{n=1}^K a_n^2\)
It is not very clear what one can do with this. For $a_1$ we now have a quadratic equation
\[\begin{equation} \frac{1}{2R}a_1^2+\frac{4}{\pi} a_1 +\dfrac{1}{2 R}\sum_{n=2}^K a_n^2 +\sum_{j=1}^{K/2}\frac{4a_{2j+1} }{\pi (2j+1)}=0 \end{equation}\]One can define $C=\sum_{n=2}^K a_n^2 +2R\sum_{j=1}^{K/2}\frac{4a_{2j+1} }{\pi (2j+1)}$ so that
\(a_1^2+8\dfrac{R}{\pi} a_1+C=0\) And obtain two solutions (which is a bit suspicious)
\[\begin{equation} a_1 = \dfrac{-4R}{\pi}\pm\sqrt{\dfrac{16R^2}{\pi^2}-C} \end{equation}\]This is valid if
\[\begin{equation} \dfrac{16R^2}{\pi^2}>C \end{equation}\]which constrains the coefficients of the Fourier expansion further.
Numerical test
I now just fast forward to the code (forgetting that I should prove that the coefficients are indeed Gaussian variables), and use the result above to evaluate $a_1$ and produce suitable paths.
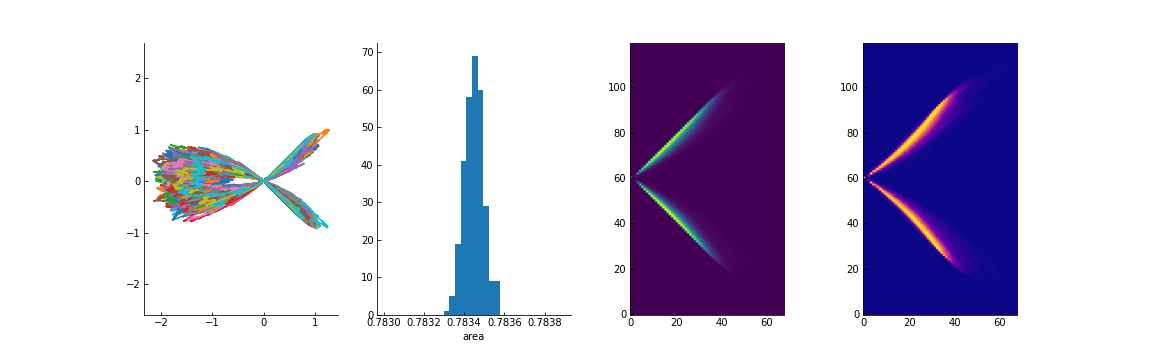
I draw 300 paths, and compute the area using shapely.
With the positive solution $a_1^+$, the equal area condition is very well satisfied, with precision down to the 4th decimal in the worst case.
High $\gamma/T=500$ , $a_1^+$

Medium $\gamma/T=50$ , $a_1^+$
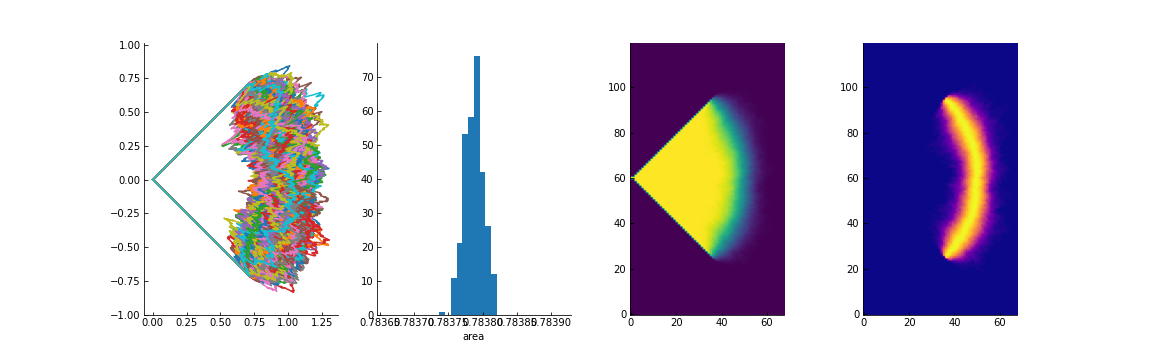
Low $\gamma/T=5 , $$a_1^+$
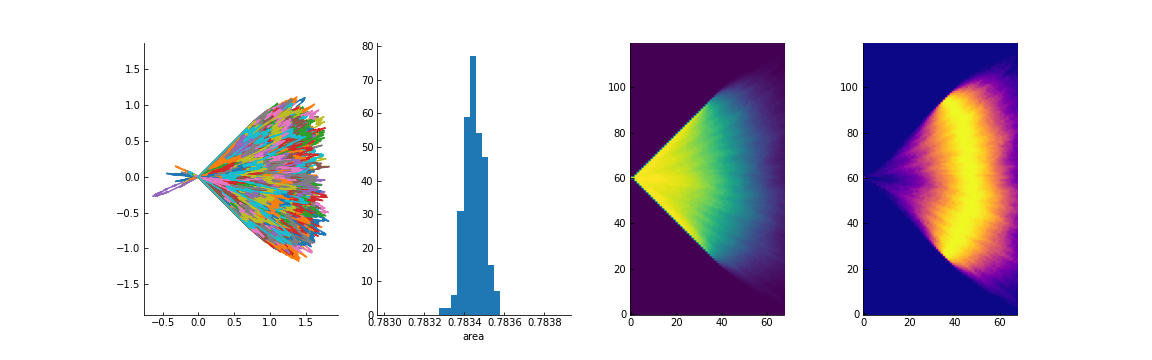
The $a_1^{-}$ solution seems not physical (it inverts the curves), even if it preserves the area rather well.
High $\gamma/T=500, a_1^-$
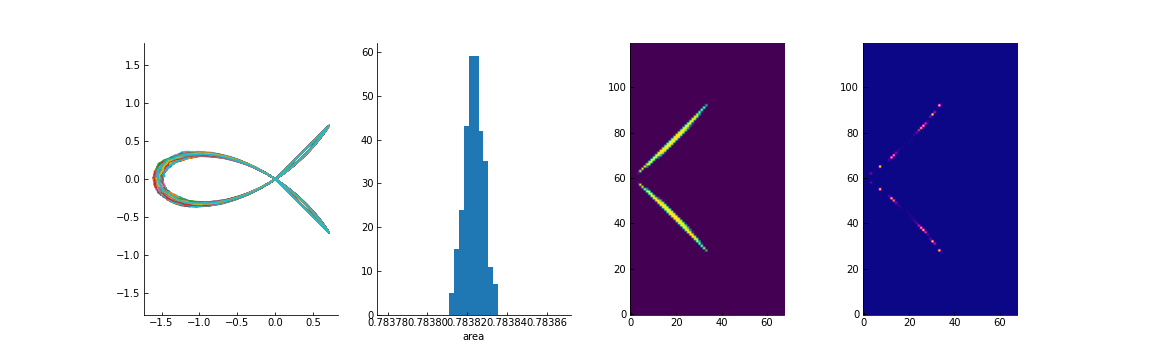
Medium $\gamma/T=50 , $$a_1^-$
Low $\gamma/T=5 , $$a_1^-$