Active particle mobility around cross-shaped barrier
We have previously seen that the a cross-shaped barrier promotes the localisation of the high density phase of phase separated active Brownian particles in a fashion that depends on the strength of the barrier.
What about the mobility of particles around the barrier?
Trajectories around the barrier
In 2D it is particularly easy to visualise the trajectories of particles around the barrier
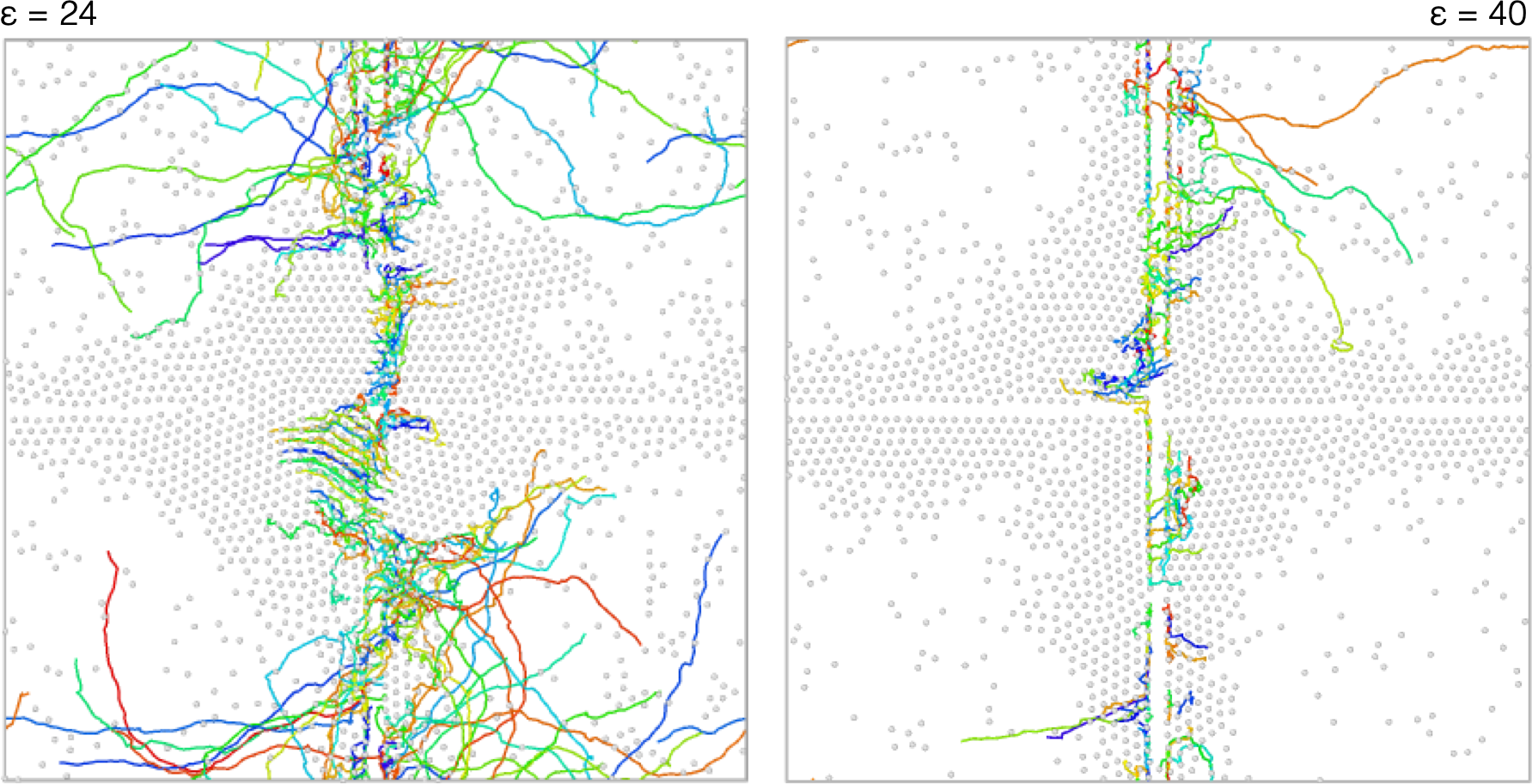
A few observations:
- The barriers promote longitudinal motion: stronger barriers are more effective than weaker barriers
- Weak barriers allow for the formation of dense domains across the barriers: these move collectively, in a way that is influenced by the cross-shape of the object (the motion is away from the barrier)
- At low barrier strength, the high and low-density regions display different patterns of motion: at low density, the barrier promotes longitudinal motion, at high density, much less so.
In simple words, particles push each other across the barrier and transport occurs in the high density phase. Transport is, however, collective, it involves large regions of the high denisty phase, and it is much slower than the free motion in the low-density phase.
I would expect these effects to be even more pronounced in 3D due to the density difference.
Quantification of fluxes in the single barrier case
To be more quantitative, I have studied in 3D the original geometry of the fluxes in the simple case of a single barrier. What I wanted to check was:
- that there is no net current in the system
- how the mobility across the barrier is affected as the barrier is reduced across the asymmetry transition.
What I have done is to run trajectories to a steady state and then track the motion of the particles with a very fine resolution in time (0.05 $\tau_r$). Then i count the number of particles which change side of the barrier between two frames and therefore track the left-to-right and right-to-left flows.
The result (below) shows that there is no net flux for any value of the barrier strength, not even in the asymmetric case (hence, the asymmetric density profile does not correspond to a rectification of the dissipation). The two contributions to the current, however, increase continuously as the barrier strength is reduced (remember that the transition in 3D is around 20).
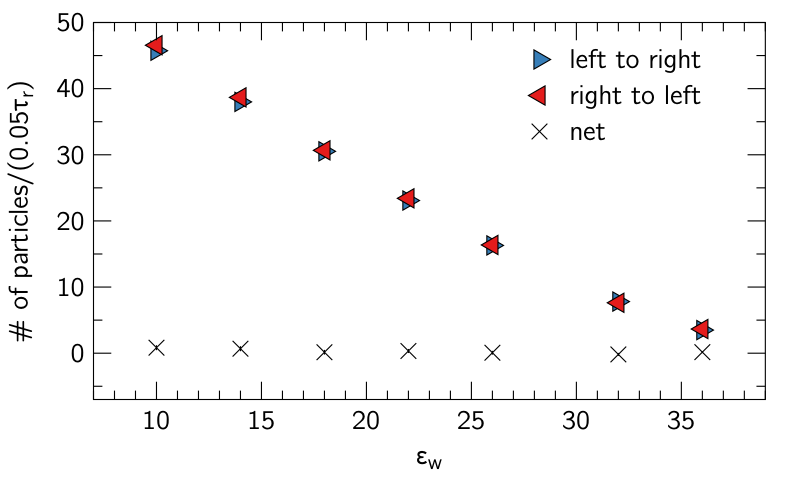
The activity at the barrier (i.e. the sum of the absolute values of the fluxes) seems to decrease almost linearly (or weakly quadratically) with the increasing barrier strength. It appears that the fluxes are not particularly sensitive to the change in the symmetry of the density profiles.
This suggests that, despite their importance for the formation of the high-density phase and its persistence at the barrier, the fluxes may not be particularly informative, and a description in terms of stationary profiles may still be the most adequate of the options.