1 Introduction to phase behaviour and enhanced fluctuations
A phase transition can be defined as a macroscopic rearrangment of the internal constituents of a system in response to a change in the thermodynamic conditions to which they are subject. A wide variety of physical systems undergo such transitions. Understanding the properties of phase transitions is fundamental to the study of soft and complex matter, as these systems often exhibit rich and subtle transformations between different states of organization. Whether in colloidal suspensions, polymer blends, liquid crystals, or biological materials, phase transitions underpin a wide range of physical behaviours, from self-assembly and pattern formation to critical phenomena and dynamical arrest. By analysing how macroscopic phases emerge from microscopic interactions and external conditions, one gains crucial insight into the principles that govern structure, stability, and functionality in these intricate systems. As such, an understanding of phase transitions not only enriches theoretical understanding but also informs practical applications across materials science, biophysics, and nanotechnology. For these reasons we will devote a large proportion of this course to the study of phase transitions.
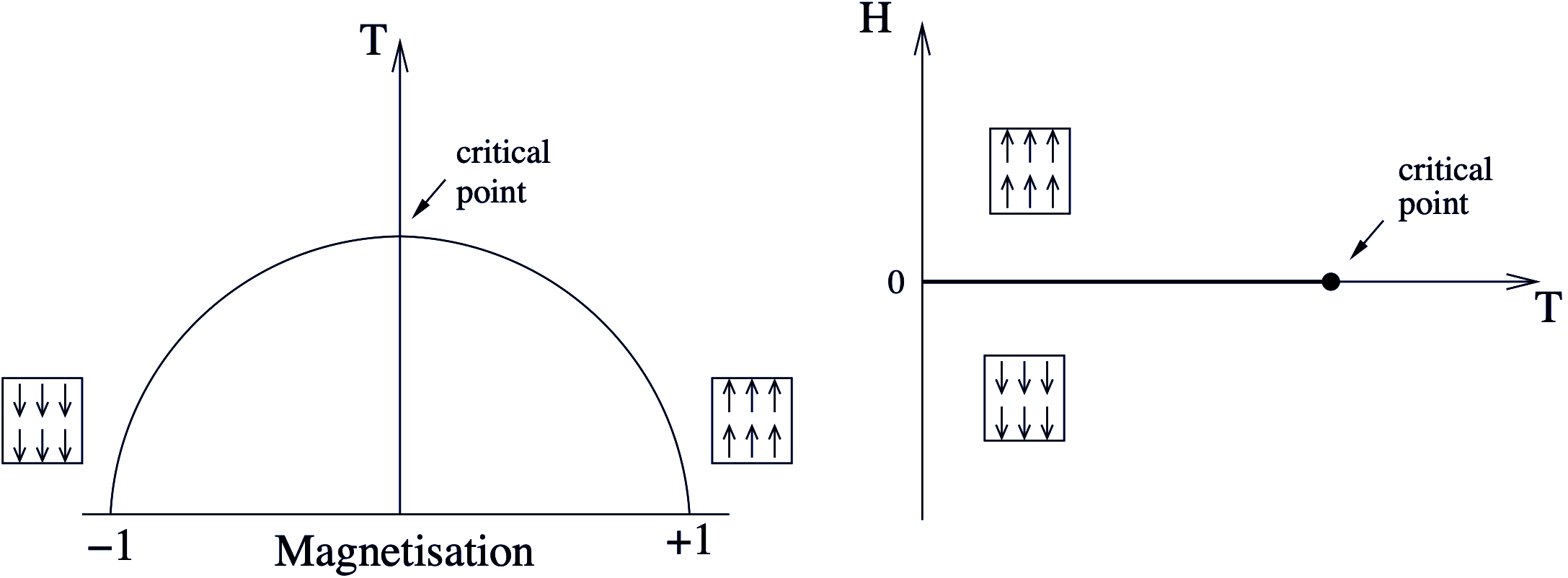
Two classic examples of systems displaying phase transitions are the ferromagnet and fluid systems. For the magnet, a key observable is the magnetisation defined as the magnetic moment per spin, given by \(m=M/N\), with \(N\) the number of spins. \(m\) can be positive or negative, dependent on whether the spins are aligned ‘up’ or ‘down’. As the temperature of a ferromagnet is increased, its net magnetisation \(|m|\) is observed to decrease smoothly, until at a certain temperature known as the critical temperature, \(T_c\), it vanishes altogether (see left part of Figure 1.1). We define the magnetisation to be the order parameter of this phase transition.
One can also envisage applying a magnetic field \(H\) to the system which, depending on its sign (i.e. whether it is aligned (positive) or anti-aligned (negative) relative to the magnetisation axis), favours up or down spin states respectively, as shown schematically in Figure 1.1 (right part). Changing the sign of the magnetic field \(H\) for \(T<T_c\) leads to a phase transition chacterised by a discontinuous jump in \(m\). We shall explore this behaviour in more detail in section 5.
Similarly, a change of state from liquid to gas can be induced in a fluid system (though not in an ideal gas) simply by raising the temperature. Typically the liquid-vapour transition is abrupt, reflecting the large number density difference between the states either side of the transition. However the abruptness of this transition can be reduced by applying pressure. At one particular pressure and temperature the discontinuity in the density difference between the two states vanishes and the two phases coalesce. These conditions of pressure and temperature serve to locate the critical point for the fluid. We define the density difference \(\rho_{liq}-\rho_{vap}\) to be the order parameter for the liquid-gas phase transition. We shall meet order parameters for other, more complex, systems in section 5,
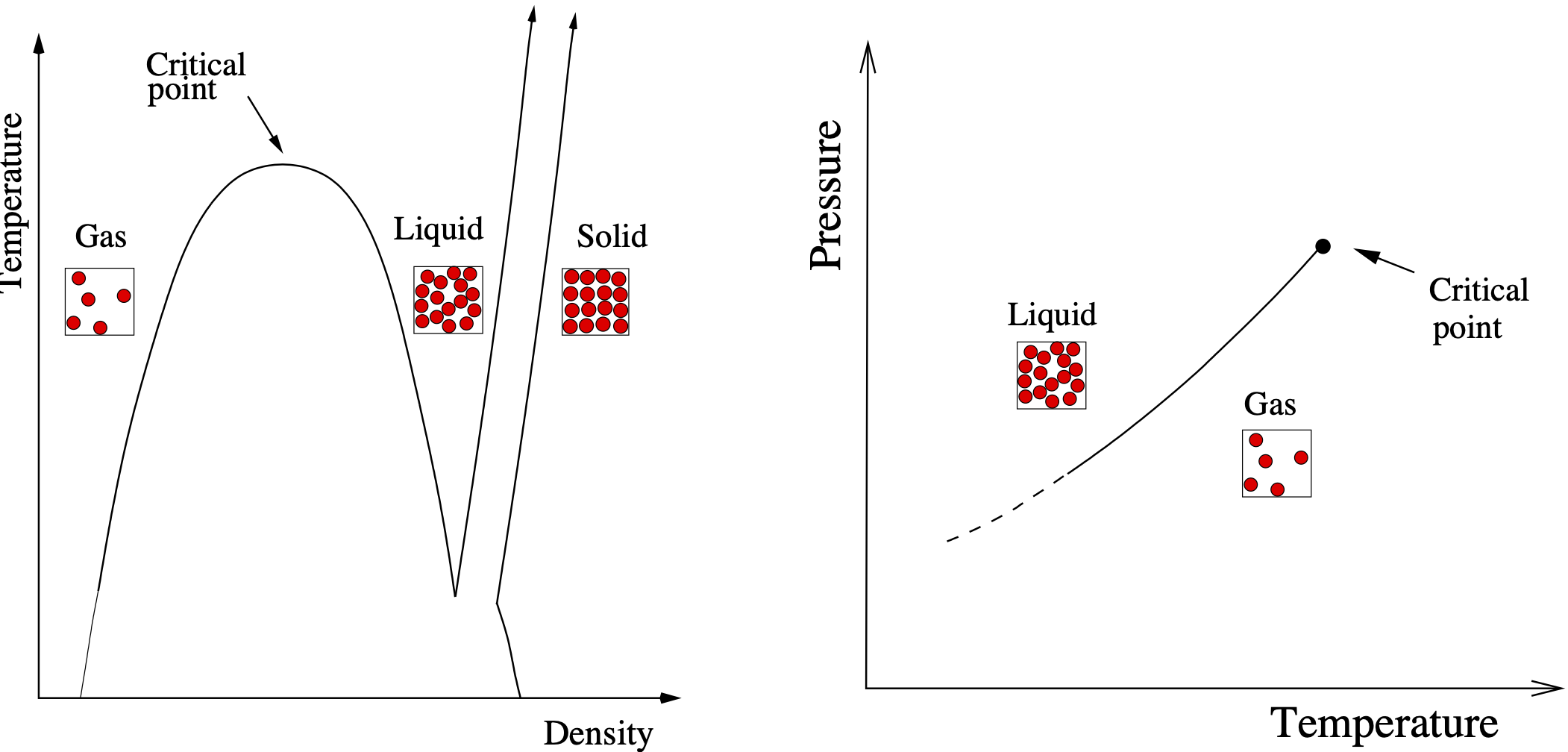
In the vicinity of a critical point, a system displays a host of remarkable behaviors known as critical phenomena. Chief among these is the divergence of thermal response functions—such as specific heat, compressibility, or magnetic susceptibility—which signal an enhanced sensitivity to external perturbations. These singularities arise from the emergence of large-scale cooperative interactions among the system’s microscopic constituents, as measured by a diverging correlation length (see Chapter 2). One visually striking manifestation of this is critical opalescence, particularly observed in fluids like CO\(_2\). As carbon dioxide nears its critical temperature and pressure, the distinction between its liquid and gas phases vanishes, giving rise to huge fluctuations in density. These fluctuations scatter visible light, rendering the fluid milky or opalescent. This scattering effect directly reflects the long-range correlations developing within the fluid. The movie below illustrates the effect as the critical temperature of CO\(_2\) is approached from above. Note the appearence of a liquid-vapour interface (meniscus) as the system enters the two-phase region.
The recalcitrant problem posed by the critical region is how best to incorporate such collective effects within the framework of a rigorous mathematical theory that affords both physical insight and quantitative explanation of the observed phenomena. This matter has been (and still is!) the subject of intense theoretical activity.
The importance of the critical point stems largely from the fact that many of the phenomena observed in its vicinity are believed to be common to a whole range of apparently quite disparate physical systems. Systems such as liquid mixtures, superconductors, liquid crystals, ferromagnets, antiferromagnets and molecular crystals may display identical behaviour near criticality. This observation implies a profound underlying similarity among physical systems at criticality, regardless of many aspects of their distinctive microscopic nature. These ideas have found formal expression in the so-called ‘universality hypothesis’ which, since its inception in the 1970s, has enjoyed considerable success.
In the next few lectures, principal aspects of the contemporary theoretical viewpoint of phase transitions and critical phenomena will be reviewed. Mean field theories of phase transitions will be discussed and their inadequacies in the critical region will be exposed. The phenomenology of the critical region will we described including power laws, critical exponents and their relationship to scaling phenomena. These will be set within the context of the powerful renormalisation group technique. The notion of universality as a phenomenological hypothesis will be introduced and its implications for real and model systems will be explored. Finally, the utility of finite-size scaling methods for computer studies of critical phenomena will be discussed, culminating in the introduction of a specific technique suitable for exposing universality in model systems. Thereafter we will consider some foundational concepts in the dynamics of complex disordered matter. We shall look at the processes by which one phase transform into another and introduce differential equations that allow us to deal with the inherent stochasticity of thermal systems. The wider applicability of these unifying concepts to complex disordered systems such as colloids, polymers, liquid crystals and glasses will be covered in part 2 of the course.